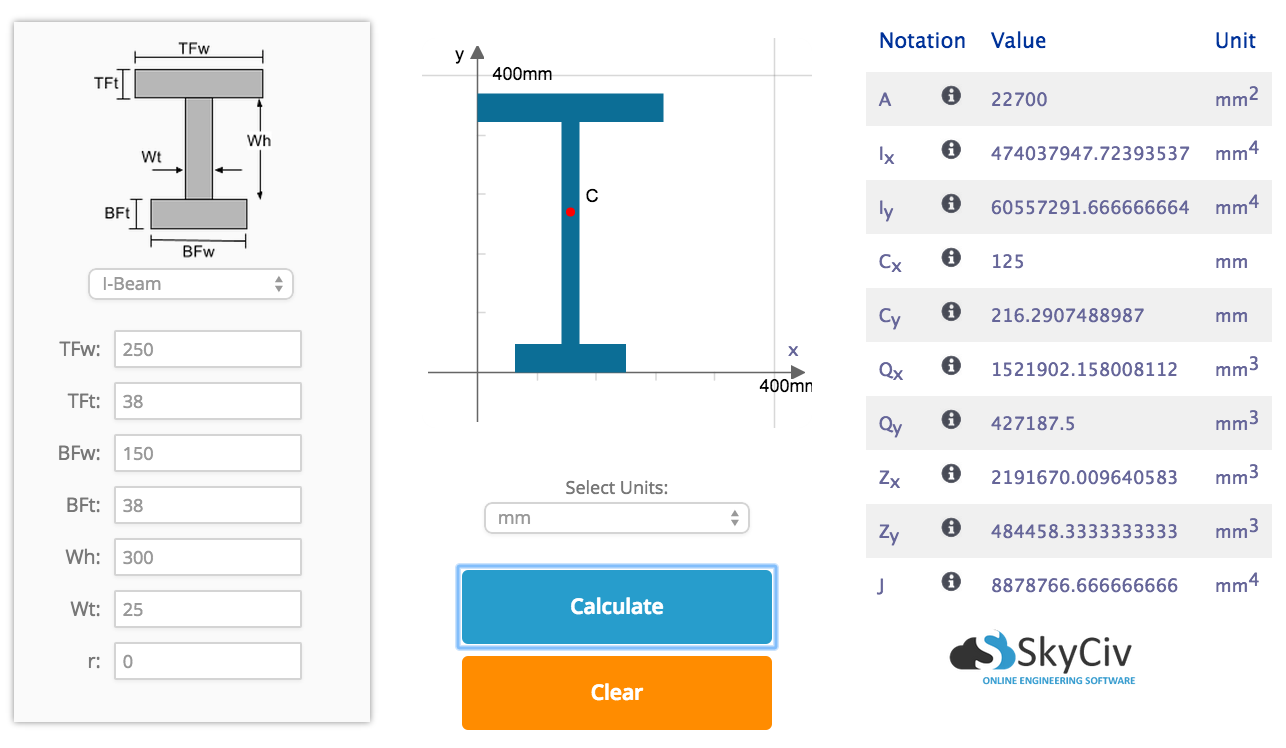
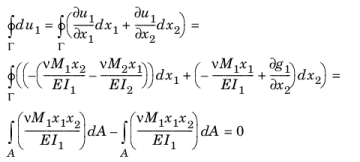Applied Sciences | Free Full-Text | Finite Element Analysis of Reinforced Concrete Beams Prestressed by Fe-Based Shape Memory Alloy Bars
Solved 100 mm 12 mm t M 12 mm 12 mm The figure above shows a | Chegg.com
Calculating Effective Rigidities of a Laminated Composite Beam (Classical Laminate Theory) | Unmanned Engineeria blog
Sectional Analysis Procedure for Reinforced Concrete Members Subjected to Pure Torsion
Schematic of the beam section and beam reference axis. | Download Scientific Diagram
Moment of Inertia of I/H Section | calcresource
Theory | C2.2 Composite Beams | Solid Mechanics II
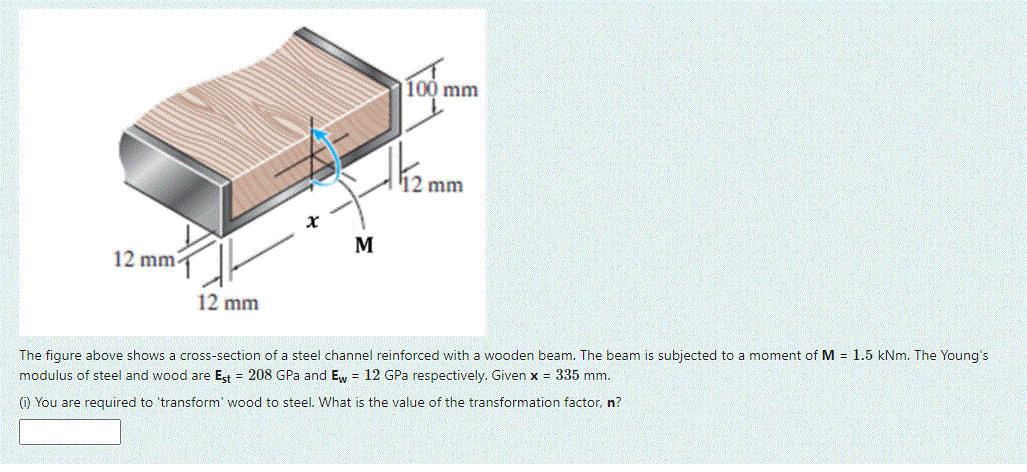
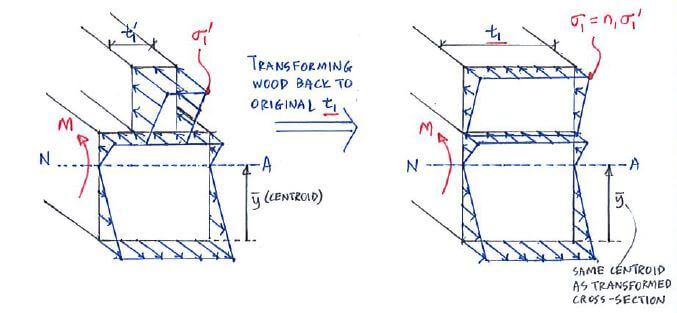
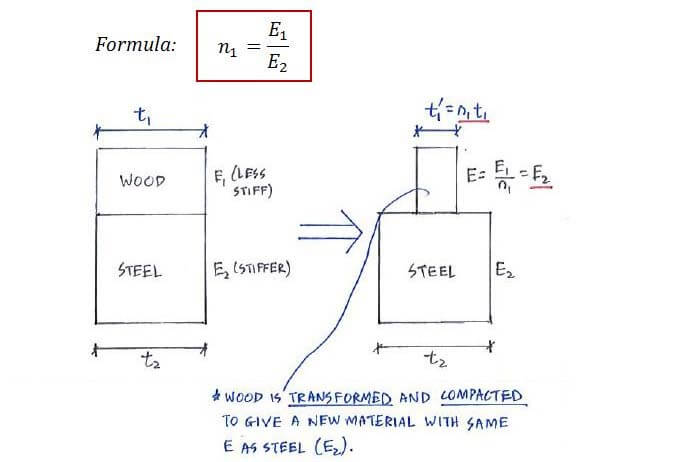
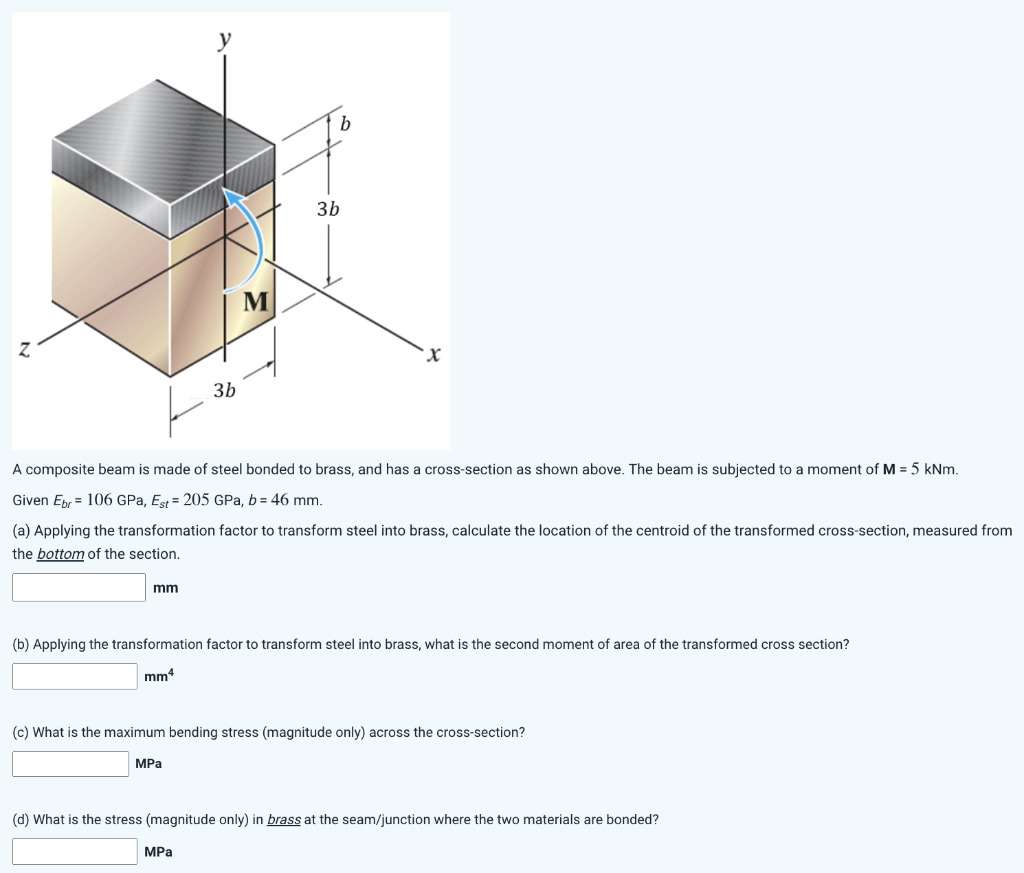
6.6 COMPOSITE BEAMS • Transformed homogeneous beam obtained through a transformation factor: Transformed-section method
Analysis of a beam cross-section under coupled actions including transversal shear - ScienceDirect
![PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/be8082b5b0ba2dac0261d012d84c39a01b5d9349/3-Figure2-1.png "PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar")
PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar
Theory | C2.2 Composite Beams | Solid Mechanics II
Transformed Area Method for Composite Beams - Mechanics of Materials - YouTube
Shear Stress Calcuation and Profile for I-beam Example - Mechanics of Materials - YouTube
Cross section (physics) - Wikipedia
5.9 Composite Beams | Bending of Beams | InformIT
Gaussian beam - Wikipedia
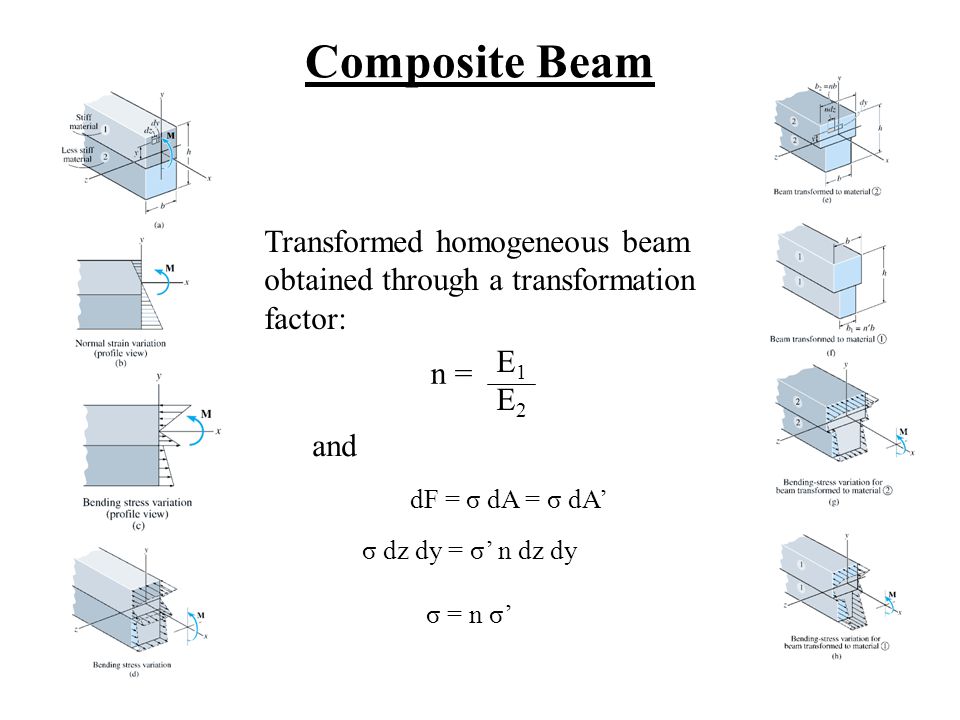
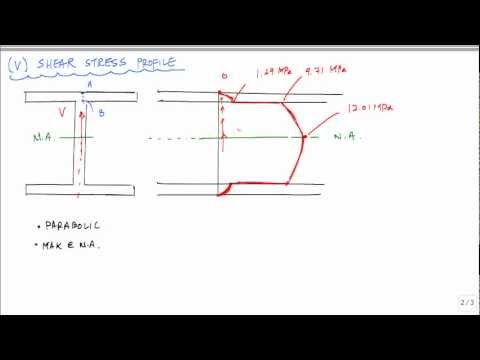
Composite Beam Transformed homogeneous beam obtained through a transformation factor: n = E1E2E1E2 dF = σ dA = σ dA' σ dz dy = σ' n dz dy σ = n σ' and. - ppt download
PDF) Buckling and vibration of axially functionally graded nonuniform beams using differential transformation based dynamic stiffness approach | suri a - Academia.edu
Solved The composite beam is made of steel (top) bonded to | Chegg.com
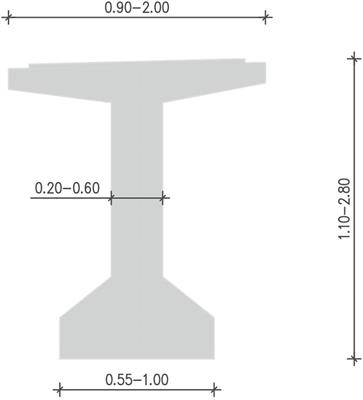
Frontiers | Proposal for the Promotion of Standardization of Precast Beams in Highway Concrete Bridges
Nonlinear analysis of shape memory alloy beam under the thermal and the mechanical loads
![PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/be8082b5b0ba2dac0261d012d84c39a01b5d9349/2-Figure1-1.png "PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar")
PDF] Vibration of a circular beam with variable cross sections using differential transformation method | Semantic Scholar
A composite beam is made of steel bonded to brass, | Chegg.com
Equations of motion of rotating composite beam with a nonconstant rotation speed and an arbitrary preset angle | SpringerLink
Free Moment of Inertia & Centroid Calculator | SkyCiv
